I. Réamhrá
Is féidir le huisce coinnle a lasadh, an bhfuil sé fíor? Is fíor é!
An bhfuil sé fíor go bhfuil eagla ar nathracha roimh fhíor-ghráin? Is bréag é!
Seo a bheidh á phlé againn inniu:
Is féidir le cur isteach cruinneas tomhais a fheabhsú, an bhfuil sé fíor?
Faoi ghnáththosca, is é cur isteach namhaid nádúrtha na tomhais. Laghdóidh cur isteach cruinneas na tomhais. I gcásanna tromchúiseacha, ní dhéanfar an tomhas i gceart. Ón dearcadh seo, is féidir le cur isteach cruinneas na tomhais a fheabhsú, rud atá bréagach!
Ach an amhlaidh atá i gcónaí? An bhfuil cás ann nach laghdaíonn cur isteach cruinneas an tomhais, ach ina ionad sin feabhsaíonn sé é?
Is é an freagra tá!
2. Comhaontú Idirghabhála
I dteannta leis an staid iarbhír, déanaimid an comhaontú seo a leanas maidir leis an gcur isteach:
- Níl comhpháirteanna DC sa chur isteach. Sa tomhas iarbhír, is cur isteach AC den chuid is mó atá i gceist, agus tá an toimhde seo réasúnta.
- I gcomparáid leis an voltas DC tomhaiste, tá aimplitiúid an trasnaíochta sách beag. Tá sé seo ag teacht leis an staid iarbhír.
- Is comhartha tréimhsiúil é cur isteach, nó is ionann an meánluach agus nialas laistigh de thréimhse ama socraithe. Ní gá go mbíonn an pointe seo fíor i dtomhas iarbhír. Mar sin féin, ós rud é gur comhartha AC minicíochta níos airde é an cur isteach i gcoitinne, i gcás an chuid is mó de na cur isteach, is réasúnta an coinbhinsiún maidir le meán nialasach ar feadh tréimhse ama níos faide.
3. Cruinneas tomhais faoi chur isteach
Úsáideann formhór na n-ionstraimí tomhais agus na méadair leictreacha tiontairí AD anois, agus tá dlúthbhaint ag a gcruinneas tomhais le rún an tiontaire AD. Go ginearálta, bíonn cruinneas tomhais níos airde ag tiontairí AD a bhfuil rún níos airde acu.
Mar sin féin, bíonn rún AD teoranta i gcónaí. Ag glacadh leis go bhfuil rún AD 3 ghiotán agus gurb é 8V an voltas tomhais is airde, is ionann an tiontaire AD agus scála atá roinnte ina 8 roinn, agus is ionann gach roinn agus 1V. Is slánuimhir i gcónaí toradh tomhais an AD seo, agus iompraítear nó caitear an chuid deachúil i gcónaí, agus glactar leis go n-iompraítear é sa pháipéar seo. Beidh earráidí tomhais mar thoradh ar iompar nó ar chaitheamh amach. Mar shampla, tá 6.3V níos mó ná 6V agus níos lú ná 7V. Is é 7V toradh tomhais AD, agus tá earráid 0.7V ann. Tugtar earráid chainníochtúcháin AD ar an earráid seo.
Ar mhaithe le háisiúlacht na hanailíse, glacaimid leis nach bhfuil aon earráidí tomhais eile ag an scála (tiontaire AD) seachas an earráid chainníochtúcháin AD.
Anois, úsáidimid dhá scála chomhionanna den sórt sin chun an dá voltas DC a thaispeántar i bhFíor 1 a thomhas gan cur isteach (cás idéalach) agus le cur isteach.
Mar a thaispeántar i bhFíor 1, is é 6.3V an voltas DC iarbhír a tomhaiseadh, agus níl aon chur isteach ar an voltas DC sa fhigiúr ar chlé, agus is luach tairiseach é. Taispeánann an figiúr ar dheis an sruth díreach a chuireann an sruth ailtéarnach isteach air, agus tá luaineacht áirithe sa luach. Tá an voltas DC sa léaráid ar dheis cothrom leis an voltas DC sa léaráid ar chlé tar éis an comhartha cur isteach a dhíchur. Léiríonn an chearnóg dhearg sa fhigiúr toradh tiontaithe an tiontaire AD.

Voltas DC idéalach gan cur isteach
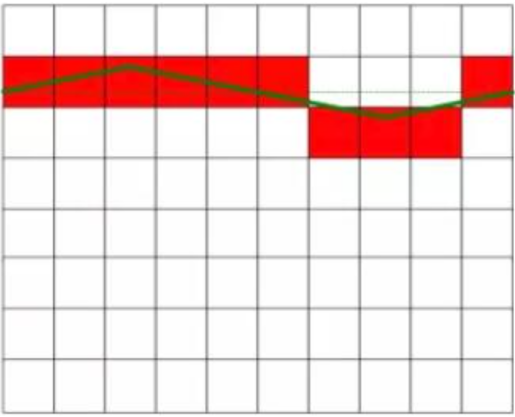
Cuir voltas DC trasnaíochta i bhfeidhm le meánluach nialas
Déan 10 dtomhas den sruth díreach sna dhá chás sa fhigiúr thuas, agus ansin déan meán na 10 dtomhas.
Déantar an chéad scála ar chlé a thomhas 10 n-uaire, agus bíonn na léamha mar a chéile gach uair. Mar gheall ar thionchar earráid chainníochtúcháin AD, is é 7V gach léamh. Tar éis meán 10 dtomhais, bíonn an toradh fós 7V. Is é 0.7V an earráid chainníochtúcháin AD, agus is é 0.7V an earráid tomhais.
Tá an dara scála ar dheis athraithe go mór:
Mar gheall ar an difríocht idir dearfach agus diúltach an voltais trasnaíochta agus an aimplitiúid, bíonn an earráid chainníochtúcháin AD difriúil ag pointí tomhais éagsúla. Faoi athrú na hearráide cainníochtúcháin AD, athraíonn toradh an tomhais AD idir 6V agus 7V. Bhí seacht gcinn de na tomhais 7V, ní raibh ach trí cinn 6V, agus ba é 6.3V meán na 10 dtomhas! Is é 0V an earráid!
Déanta na fírinne, níl aon earráid dodhéanta, mar sa domhan oibiachtúil, níl aon 6.3V dian ann! Mar sin féin, tá go deimhin:
I gcás gan aon chur isteach, ós rud é go bhfuil gach toradh tomhais mar an gcéanna, tar éis meán de 10 dtomhas a fháil, fanann an earráid gan athrú!
Nuair a bhíonn méid cuí cur isteach ann, tar éis meánú 10 dtomhas, laghdaítear an earráid chainníochtúcháin AD faoi ord méide! Feabhsaítear an taifeach faoi ord méide! Feabhsaítear cruinneas an tomhais faoi ord méide freisin!
Is iad na príomhcheisteanna ná:
An mar an gcéanna é nuair a bhíonn luachanna eile ag an voltas tomhaiste?
B’fhéidir gur mhaith le léitheoirí an comhaontú maidir le cur isteach sa dara cuid a leanúint, an cur isteach a chur in iúl le sraith luachanna uimhriúla, an cur isteach a fhorchur ar an voltas tomhaiste, agus ansin torthaí tomhais gach pointe a ríomh de réir phrionsabal iompair an tiontaire AD, agus ansin an meánluach a ríomh le haghaidh fíoraithe, fad is féidir leis an aimplitiúid cur isteach an léamh tar éis cainníochtú AD a athrú, agus go bhfuil an mhinicíocht samplála ard go leor (bíonn próiseas aistrithe ag athruithe aimplitiúid cur isteach, seachas dhá luach dearfach agus diúltach), agus ní mór an cruinneas a fheabhsú!
Is féidir a chruthú, fad is nach slánuimhir go díreach an voltas tomhaiste (níl sé ann sa domhan oibiachtúil), go mbeidh earráid chainníochtúcháin AD ann, is cuma cé chomh mór is atá an earráid chainníochtúcháin AD, fad is mó a bhíonn aimplitiúid an chur isteach ná an earráid chainníochtúcháin AD nó níos mó ná an taifeach íosta de AD, cuirfidh sé faoi deara go n-athróidh toradh an tomhais idir dhá luach cóngaracha. Ós rud é go bhfuil an cur isteach dearfach agus diúltach siméadrach, tá méid agus dóchúlacht an laghdaithe agus an mhéadaithe cothrom. Dá bhrí sin, nuair a bhíonn an luach iarbhír níos gaire don luach sin, is mó an dóchúlacht go mbeidh an luach sin le feiceáil, agus beidh sé gar don luach sin tar éis meánú.
Is é sin: ní mór meánluach iltomhais (is é nialas an meánluach cur isteach) a bheith níos gaire don toradh tomhais gan cur isteach, is é sin, is féidir le comhartha cur isteach AC le meánluach nialas agus meánú iltomhais na hearráidí Cainníochtaithe AD coibhéiseacha a laghdú, réiteach tomhais AD a fheabhsú, agus cruinneas tomhais a fheabhsú!
Am an phoist: 13 Iúil 2023




